WFEM in Tire Dynamics: A Smarter Way to Model High-Frequency Vibrations

When analyzing vibrations in complex structures, especially at low frequencies, engineers often rely on eigenfrequencies and their corresponding mode shapes to understand how and why a structure behaves the way it does. These natural frequencies offer valuable insights and form the foundation for forced response calculations using modal superposition. However, as we move into higher frequencies, this classical approach begins to lose its edge. The number of modes drastically increases, and their patterns become increasingly chaotic, and the physical intuition we once had starts to fade. Also, damping, often negligible at lower frequencies, takes centre stage, influencing the response in ways that are harder to predict.

At this point, it becomes important to shift perspective.

Instead of interpreting vibrations as isolated modal frequencies paired with distinct mode shapes, we begin to see them as groups of modes that collectively resemble waves propagating through the structure. Such a wave-based perspective becomes especially meaningful when analyzing structures that are long, uniform, and directionally consistent, such as rail tracks, pipelines, or tires. These structures effectively act as waveguides, channelling the propagation of mechanical waves along their length. This wave-based view becomes not just insightful, but incredibly powerful. Enter the Waveguide Finite Element Method (WFEM) — a computationally highly efficient technique that transforms our understanding of high-frequency vibrations in elongated structures.

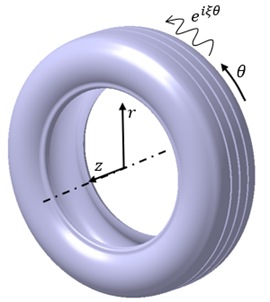
The formulation of the WFEM is built on a clever hybrid approach: it merges the numerical precision of Finite Element Analysis (FEA) with the mathematical elegance of analytical wave propagation. In this framework, FEA is used to compute displacements across the cross-section of the waveguide, while wave behavior along its length is described using analytical expressions – typically involving exponential terms like e^iξθ where ξ represents the wavenumber. When applied to a tire, the circumferential direction can be treated as the waveguide direction. This insight offers a substantial computational advantage: instead of meshing the entire 3D geometry, WFEM reduces the problem to a 2D cross-sectional mesh, drastically lowering the number of degrees of freedom while still capturing the essential dynamics of the full 3D system.
The theoretical foundation of WFEM rests on Hamilton’s Principle, a fundamental concept in classical mechanics. It states that among all possible motion paths a dynamic system can take between two points in space and time, the path actually followed is the one that minimizes the total energy. From this principle, the governing equation of motion for a tire modeled using the WFE approach can be derived. It takes the following form:
[K_0+iξK_1+ ξ^2 K_2- ω^2 M]_m U=0.
In this equation:

• K_0,K_1, and K_2 are the global stiffness matrices of the waveguide cross-section.
• M is the global mass matrix.
• ξ is the wavenumber, and ω is the circular frequency.
• The subscript m denotes the total number of degrees of freedom associated with the waveguide’s cross-section.
• U is the nodal displacement amplitude vector, representing the unknown wave modes across the section.

The governing WFE equation typically results in a twin-parameter eigenvalue problem, where both the wavenumber (ξ) and the frequency (ω) play central roles. Depending on the analysis goal, one can approach this problem in two ways: by solving a linear eigenvalue problem for a given wavenumber, or a quadratic eigenvalue problem for a specified frequency.

Moreover, the elegance of the WFE framework lies in its flexibility to incorporate nonlinear elastic behavior. When dealing with complex structures like tires, it becomes crucial to account for both material nonlinearity (such as the hyperelastic behavior of rubber) and geometric nonlinearity (arising from large deformations due to inflation pressure). In such cases, the stiffness matrices in the WFE formulation are no longer constant. Instead, they are split into components: the tangential stiffness matrix, which captures incremental stiffness around a deformed configuration, and the initial stress stiffness matrix, which reflects the influence of the pre-stressed state. To compute these modified matrices, a two-step approach is generally adopted. First, a nonlinear static analysis is conducted to simulate the deformation of the tire under inflation, capturing its pre-deformed, stressed state. The resulting data is then used to construct updated stiffness matrices, which feed into the dynamic wave analysis.

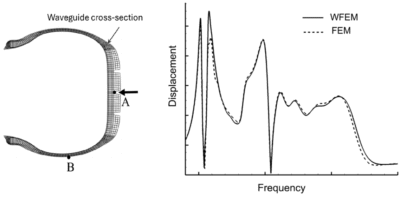
The figure illustrates the accuracy WFE method by comparing its results with those from a conventional full 3D FEA model. It presents the Frequency Response Function (FRF), computed by applying a unit nodal force at location A and measuring the resulting displacement response at location B. Despite the absence of axis values due to proprietary restrictions, the overlay demonstrates excellent agreement between the WFE and traditional FE results- validating the reliability of the waveguide approach. What makes WFE particularly powerful is its computational efficiency. By reducing the problem to a 2D cross-sectional analysis, the size of the matrices involved is drastically smaller than those in a full 3D FE model, enabling faster and more memory-efficient simulations. In addition to FRF analysis, the WFE framework also enables the derivation of dispersion curves, which are particularly valuable for high-frequency vibration analysis. Such dispersion curves, which relate frequency to wavenumber, provide deep insights into wave propagation characteristics, such as phase velocity, group velocity, and cut-off frequencies.

The Waveguide Finite Element Method is not just a theoretical tool — it’s a practical, scalable, and highly efficient approach to solving complex vibration problems in elongated structures. The entire WFE framework can be implemented using computational platforms like MATLAB or Python, or by leveraging the advanced capabilities of commercial FE software such as Abaqus, through customized subroutines and scripting.

At VIAS3D, we possess the expertise and infrastructure to develop these models from the ground up and implement them in real-world applications with precision and efficiency.

Have a challenging vibration or dynamics problem in your structure? Let’s talk! Share your problem with us — we’re passionate about turning complex engineering challenges into elegant solutions. Reach out today and see how WFE can transform your analysis.

📩 Contact us at: achakraborty@vias3d.com — we’d be happy to help!

Contributors:

VIAS3D Engineering Services Team

Madhavrao Londhe, FEA Engineer, VIAS3D

He is a Mechanical Engineer with over five years of experience in Abaqus, MATLAB, and tire simulations. He has worked on various projects for the tire industry, focusing on development of customized simulation techniques. His expertise spans solid mechanics, linear and nonlinear FEA, computational modelling, experimental techniques, and new product design and development. Additionally, he has three years of work experience in the medical equipment industry.

Murthy Lakshmiraju, PhD, Director of Engineering Consulting at VIAS3D

Murthy Lakshmiraju, Ph.D. has over 15 years of advanced use and experience in CFD to solve real life engineering problems for numerous industries, including appliances, energy, oil and gas, marine and chemical processing. He graduated with a Masters and Ph.D. in Mechanical Engineering from Tennessee Tech, USA. He has experience in different flow physics, including advanced turbulence modeling, multiphase flow, heat transfer, Dynamic Fluid Body Interaction (DFBI), Fluid Structure Interaction (FSI), Chimera mesh, Conjugate Heat Transfer (CHT) and reacting flows with combustion and emission modeling.

Arindam Chakraborty, PhD, PE, CTO Engineering Consulting at VIAS3D

He is a mechanical engineer with more than 12 years of strong academic and consulting experience in solid mechanics and design, non-linear FEA, fatigue and fracture mechanics, reliability analysis, composite structures in Oil C Gas, Nuclear, and Structural Design. He holds degrees in Civil (E), Aerospace (MTech), and Mechanical (PhD). He has a strong background in project management, business development, strategy development, and technology development, with a strong focus on public safety regulations (BSEE, NRC). Dr. Chakraborty has strong technical knowledge and working skills in CAE techniques and widely known solutions like Abaqus. He has experience in automating complex engineering problems using codes in FORTRAN/C/C#/VBA/Java/Python GUI scripts. Dr. Chakraborty has more than 25 conference and journal publications, including invited talks at industry conferences and academia. He is closely involved with ASME and API Codes C Standards committees and task groups.